An adjustable alternative to the SmoothStep function

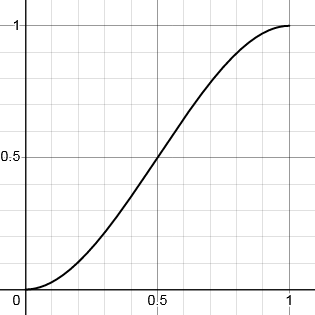
SmoothStep is a useful sigmoid function that interpolates between (0,0) and (1,1). It is monotonically increasing, has 0 gradient at the start and end, and passes through (0.5,0.5) with gradient 1.5.

y = 3x² - 2x³

But sometimes you want to be able to vary the shape of the curve – to change the steepness of the slope or the position of the inflexion point.

Good news!

Here is a function that does all these things. The curve passes through the inflexion point (p,p) with gradient g. You can adjust these parameters to shape the curve to your requirements.

c(g) = (g - 1) / (2 - g)

f(x, p, c) = x((x + xc) / (x + pc))

for 0 ≤ x < p, y = f(x, p, c(g))

for p ≤ x ≤ 1, y = 1 - f(1-x, 1-p, c(g))

p = 0.5, g = 1.5

p = 0.5, g = 5

p = 0.2, g = 2

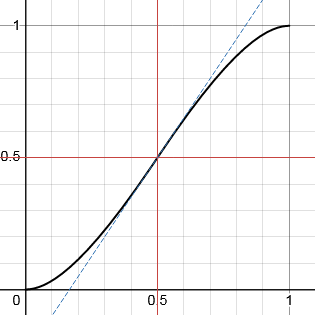
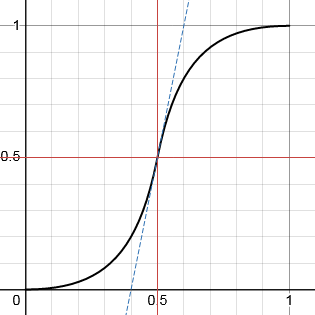
As you can see, p = 0.5, g = 1.5 gives a curve very similar to SmoothStep (although not identical).

When programming, care must be taken to cope with the discontinuity in the calculation of c, at the value of g = 2. Clamping the infinte value to a large number gives an acceptable result

You can play around with the parameters on a graph here: https://www.desmos.com/calculator/dkvvdyomfl

But we can go even further

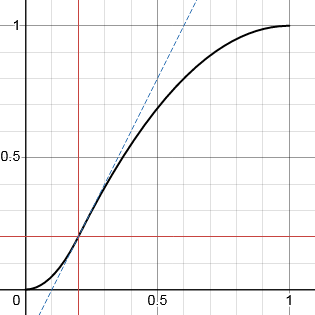
In all the curves above, the x and y co-ordinates of the inflexion point are tied to the same value. The function can be refined to break this restriction and allow the inflexion point to be freely specified as (p,q).

c(g) = (g - 1) / (2 - g)

f(x, p, c) = x((x + xc) / (x + pc))

for 0 ≤ x < p, y = (q/p)f(x, p, c((p/q)g))

for p ≤ x ≤ 1, y = 1 - ((1-q)/(1-p))f(1-x, 1-p, c(((1-p)/(1-q))g))

p = 0.4, q = 0.2, g = 2

p = 0.4, q = 0.4, g = 2

p = 0.4, q = 0.6, g = 2

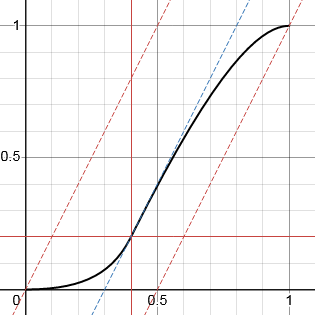
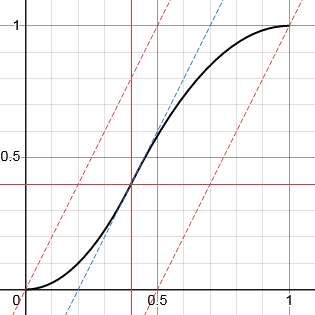
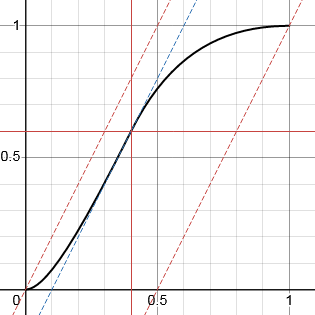
Note that the values p, q, and g are not totally independent. To preserve monotonicity and the start and end 0 gradients, the point (p,q) must lie between a line of gradient g passing through (0,0) and one passing through (1,1). I have chosen to implement this as a limit on the value of q.

q' = min(max(q, (p - 1)g + 1), pg)

You can play around with the parameters on a graph here: https://www.desmos.com/calculator/9r0vuweiyj

A rose by any other name

You can call it "adjustable SmoothStep" or "tunable SmoothStep" or "variable SmoothStep" if you want. Or not, if you don't, since it's not exactly identical, even though it is close in shape. Whatever you call it, I hope this flexible interpolation function is useful to you.

Enjoy! (^_^)